1. Introduction
Accurate estimation of total electron content (TEC) in the ionosphere has many applications in various domains. Some of these are GNSS positioning, applications for space weather, analysis of various traveling ionospheric disturbances (TID), e.g., co-seismic ionospheric disturbances (CID), or the determination of ionospheric correction for low-Earth orbit (LEO) satellites. This last application is investigated in this study; more precisely, the use of TEC for calculating ionospheric corrections for radar altimetry, where measuring the distance to the Earth requires especially high accuracy. This accuracy is attained partially by very accurate orbits, but a significant number of the corrections, including ionospheric correction, also should not degrade this accuracy (Fu, Cazenave 2001). Although the dual frequency altimeters determine ionospheric delay, the signal is noisy and difficult to use over inland and shallow waters. We need better ionospheric corrections for coastal regions and for inland altimetry, which is an even more, novel geophysical field. Therefore, in this study, we compare ionospheric delays from dual-frequency altimeters and those calculated from the GIMs, which are modeled from different data densities but cover the entire Earth.
The ionospheric correction for the altimetry-derived range to the ocean can be estimated directly from dual-frequency altimeters, but single-frequency missions require TEC models for this purpose. The dual-frequency altimetry missions determine TEC and ionospheric corrections over the oceans, but leave empty places over land areas. The dual-frequency GNSS observations from ground stations are available only from sparse stations over the oceans, and therefore GNSS-based GIM is worse over the oceans. Thus, altimetry-derived TEC and GNSS-derived TEC are complementary. This means that GIMs from GNSS modeled by different techniques can be validated over the seas by TEC from altimetry, and inversely, GIMs provide ionospheric delay everywhere, including areas where determination from the altimeters is impossible.
There is a large record of studies referring to ionospheric delay acquired from altimetry and ground-based GNSS. Many studies apply these two observational techniques together with other ancillary data like Doppler Orbitography and Radiopositioning Integrated by Satellite (DORIS), GNSS from topside antennas, or occultation GNSS measurements. Some studies combine different observations in the creation of TEC models, both local ones and the GIMs. An example of combined model creation can be found in Alizadeh et al. (2011), who present a GIM modeled by spherical harmonics from the ground-based GNSS, Jason-1 altimetry, and Formosat-3/COSMIC data. The authors discuss, in particular, the effect of including alti-metric data in the model. Other combinations of data, but in local ionosphere modeling, can be found in Dettmering et al. (2014), who apply B-spline functions for the interpolation of data derived from terrestrial GPS, space-based GPS, altimetry from three satellites, and very-long-baseline interferometry (VLBI). Tomographic solutions, often a starting point in the creation of 2D GIMs, are additional examples of data combinations in modeling. Tang et al. (2015) solved the problem of data insufficiency in computerized ionospheric tomography (CIT) by integrating ground-based GPS data, occultation data from low Earth orbit (LEO) satellites, satellite altimetry data from Jason-1 and Jason-2, and ionosonde data. The ionospheric delay issues were also investigated recently with respect to sea surface altimetry using the Global Navigation Satellite System Reflectometry (GNSS-R) by Yan et al. (2022), who investigated GIM as the source of ionospheric correction.
The existing studies are also focused on validating various ionosphere models with independent data, which most often comes from altimetry (Ren et al. 2019; Chen et al. 2020; Wielgosz et al. 2021). One of the oldest examples was given by Azpilicueta and Brunini (2009), who analyzed the bias between TEC from the TOPEX/Poseidon mission and GPS-based TEC. The international reference ionosphere (IRI) model was also tested by Yasukevich et al. (2009) with the altimeter-based TEC from TOPEX/Poseidon and Jason-1. The consistency of higher-accuracy, kriging-based GIM, and TEC from Jason-2 altimetry was analyzed by Hernández-Pajares et al. (2017) using terrestrial GNSS from the stations located on the islands. Regional comparisons of TEC from Jason-1, Jason-2, and TEC based on the Crustal Motion Observation Network of China (CMONOC) were presented by Tseng et al. (2010).
These two sources of TEC, i.e., ground-based GNSS and altimetry, were most commonly interpreted as complementary over the oceans during the past two decades. The DORIS technique is the third useful technique in this area (Li, Parrot 2007). However, data coverage over the oceans available from the individual satellites receiving DORIS signals is sparser than from the single altimetry satellite (Dettmering et al. 2014). This fact could potentially be a reason for the more frequent application of altimetry in the validation of GIMs. The data implemented in the GIMs applied in this study are based on ground GNSS stations, which are mostly in continental areas. The ocean areas in GIMs are supported by GNSS stations on islands, which have sparse distribution. The satellite TEC data most frequently applied in GIM validation are DORIS, distributed over the continents and oceans, and dual-frequency altimetry TEC, available only over the oceans. However, in contrast to DORIS, satellite altimetry is independent of the stations, and therefore it provides continuous observations over entire ocean areas along the satellite footprints. The only problem is the small number of satellites, but currently, 3-4 are usually available, which is useful for validation purposes.
The validation and targeted enhancement of GIMs, with the application of dual-frequency altimetry over the oceans, requires comparison with altimetry in TEC units. On the other hand, applying GIM-based TEC in the calculation of ionospheric corrections for altimetric ranges requires conversion of the data from these two sources to cm. The interpolation of GIM used for the generation of ionospheric delay, which applies to single-frequency altimetry missions, other LEO missions, and inland altimetry, is mandatory if the satellite itself has no capability for determining the ionospheric delay. TOPEX/Poseidon, which originated in 1992, was one of the first dual-frequency altimetry missions. Therefore, ionosphere models could be validated from that time forward. Shortly after 1992, Bilitza et al. (1995) suggested that the International Reference Ionosphere model (IRI) could be used to determine ionospheric corrections for the altimeters onboard Geosat or ERS-1. They also compared IRI results to TOPEX/Poseidon ionospheric delay determinations. Komjathy and Born (1999) have studied the usefulness of ionosphere models based on the combination of GIM and IRI in the generation of ionospheric corrections for altimetry. They found errors in GIMs equivalent to 4 cm of altimetric range delay.
There are also critical applications of ionospheric correction that need accurate GIM models validated and consistent with the other sources of TEC-like dual-frequency altimetry or DORIS. It is critical to understand the errors between the GIMs and altimeters in the context of such applications as ocean-level trends or inland altimetry. The latter challenge is looming, given the upcoming SWOT mission (Biancamaria et al. 2016).
Dettmering and Schwadtke (2022) studied ionospheric delay accuracy in the context of reliable global mean sea level (GMSL). Their comprehensive study of ionospheric delay magnitude and its errors were analyzed from TOPEX and three Jason satellites (1-2-3) together with GIMs, such as NOAA Ionospheric Climatology (NIC09). In reference to inland altimetry, Fernandes et al. (2014) studied ionospheric corrections together with other atmospheric corrections for altimetry observation of inland waters. They tested GIMs with dual-frequency altimetric determination of the delay, which is poor over inland waters, mainly due to the large footprint of the altimetric radar pulse, and land influence on the signal. The GMSL requires especially accurate atmospheric corrections if we want to assess its trends in the short-time window. Single-frequency altimeters contribute much to this field, but need GIM-based ionospheric delay over areas where ground GNSS stations are sparse. For inland altimetry, the challenge is in determining the correct ranges where the ranging is disturbed by the presence of land. The determination of ionospheric delay from dual-frequency altimeters can be even harder inland. If we want to use GIMs, we must remember that even if GIMs use more continental ground GNSS stations, we can validate them with altimetry only in coastal zones. The comparative study of 5 models and 3 altimeters reported here was performed to provide several numerical results useful for future studies of these demanding applications.
2. Altimetry-derived ionospheric delay vs. that recalculated from Global Ionosphere Maps
Dual-frequency radar altimeters penetrate the ionosphere by first sending an electromagnetic pulse through the atmosphere, and then measuring the received response after the pulse is reflected by the ocean and propagates back to the satellite. The application of two frequencies enables the determination of ionospheric delay of pulse propagation transmitted across the ionosphere below the satellite orbit, an altitude of 1300 km for Jason satellites, and 800 km for Sentinel 3 satellites. Dual-frequency altimeters use shorter wavelengths than GNSS for determining the ionospheric correction. The radar altimeters used for Jason-2, Jason-3, and Sentinel-3 missions transmit pulses alternatively at the Ku-band (around 13.6 GHz), the main frequency for altimeter range measurements, complemented by a C-band frequency (around 5.3 GHz) that is used to correct range delay. The ionospheric correction for the range R is given for the two frequencies by the following equations:
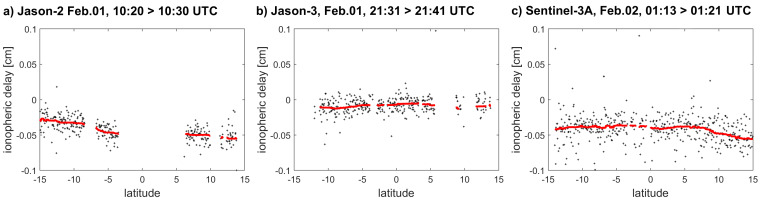
where:
where fKu and fC are respective frequencies (in Hz). The relation between TEC and ionospheric delay for the Ku-band frequency translates to about 2 mm in altitude for each TEC unit. The frequency ranges, ocean behavior, and other factors cause TEC values derived from the altimetric ranging to be characterized by significant noise, which affects the output accuracy of filtered TEC, typically by 1-2 TECU. Therefore, the filtering process has always to be applied. Because of the random character of the noise, a filter based on the moving average is often applied in practice (Hernández-Pajares et al. 2017). The window size of the moving average determines the spatial resolution of the ionospheric correction along the orbital footprint in the spectral sense, i.e., the longer the window, the longer-wavelengths of the signal can be kept. The average filtering of ionospheric delay measured along three selected tracks from three satellites is shown in Figure 1. The window size is here 80 s, which is equivalent to a ~465 km footprint at sea level or ~575 km at orbital altitude. Such filtered ionospheric delays are applicable in the computation of corrected altimetric ranges.
Fig. 1.
Selected tracks of altimetry-derived Ku-band ionospheric delay determination (black) and its smoothing by moving average with 80 s window (red).
The delay of pulse propagation induced by the ionosphere is proportional to TEC. Since ionization in the upper part of the atmosphere is primarily caused by solar ultraviolet radiation, spatial and temporal variability in the ionospheric correction is linked to solar conditions. The ionospheric corrections ionocorrGIMKu and ionocorrGIMC can be obtained from the GIM by using the first-order expansion of the refraction index (Dettmering et al. 2011):
where fKu and fC are respective frequencies (in Hz), and TEC is expressed in electrons/m2. Since the relationship between TEC and ionospheric delay is proportional, the sources of GIM-altimetry inconsistency that come from the GIMs are the interpolation of the GIM, the spatiotemporal resolution of the GIM, and its quality depending on the data and methods used. The additional bias between the GIM TEC and altimetry-derived TEC can originate from the orbital altitudes of altimetric satellites, which are different from GNSS satellite altitudes. The shapes of vertical electron density profiles have a variety of interpretations in the literature, differing much between day and night, and therefore it is not easy to derive the top-side TEC above the altimetric orbits from the models. Wielgosz et al. (2021) determined that even though adding model-derived plasmaspheric TEC does not change the standard deviation of TEC differences between the GIMs and altimetry by much, the systematic error between these two sources can reach 2 TECU, which together with filtering errors (Fig. 1) can contribute to ionospheric delay differences derived from these two techniques.
The local model was developed by the authors of this study using point TEC determination from Precise Point Positioning (PPP) (Li et al. 2013; Jarmołowski et al. 2019). The grid values were then interpolated spatially in separate epochs by least-squares collocation (LSC), and the model with spatial resolution of 1°×1° and temporal resolution of 5 min. was designated PPPLSC. The other TEC models used in the study come from IGS associate analysis centers, and contribute to the official IGS GIM, or are unique in terms of spatiotemporal resolution or modeling method, like UQRG. The UQRG global model, based on ordinary kriging, usually performs better compared with altimetry from the other models (Roma-Dollase et al. 2018; Wielgosz et al. 2021). CODG and IGSG global models based on spherical harmonics are official and popular models contributing to IGS. The JPLG model is embedded in altimetry data as a background model for dual-frequency altimetry-based delays. In this work, the altimetry trajectory samples and GIM grids are selected in the equatorial area between latitudes 15°N and 15°S, and between longitudes 90°E and 150°E (Fig. 2).
The standard spatial resolution of GIM grids is 5° in longitude and 2.5° in latitude. Temporal resolutions vary by the model. The JPLG and IGSG models have 2-hour resolution, CODG has a 1-hour interval, and UQRG has a time interval of 15 min., whereas the authors’ model PPPLSC working version was used with 5 min. resolution. However, the spatial resolution of the grids doesn’t mean that the model includes these spatial details of the TEC signal, which correspond to grid node separation. This drawback refers, in particular, to models created based on mathematical base functions, when lower orders of these functions are applied (e.g., spherical harmonics). In referring to lower orders, we mean the orders that correspond to resolution much lower than the grid resolution. Therefore the choice of modeling method is very important. The stochastic methods are more robust, as they avoid loss of resolution in the places where the data are dense, and do not cut the higher-order TEC details contrary to low-order spherical basis functions. The GIMs are typically based on GNSS data from various numbers of ground stations. The number of these stations is usually >200, but separated stations in regions of sparse data are always included, as a priority. The authors’ model PPPLSC, based on GPS data, has applied LSC, which is equivalent to simple kriging in the interpolation (Krypiak-Gregorczyk et al. 2017). The other model assessed in this study, which is interpolated by a stochastic technique, is UQRG from the Polytechnic University of Catalunya, and it applies ordinary kriging to GPS ground data (Orús et al. 2005). The JPLG model from Jet Propulsion Laboratory uses a set of horizontal basis function coefficients (Komjathy et al. 2005) for the interpolation of ground GPS/GLONASS data. The CODG model created by The Center for Orbit Determination in Europe also uses GPS/GLONASS data and interpolation by spherical harmonics expansion up to degree and order 15 (Schaer et al. 1996). IGS GIM is a combination of different GIMs (Hernández-Pajares et al. 2009). Figure 2 depicts a selected epoch of local grids extracted from 4 of 5 GIMs discussed in this work, because JPLG data were interpolated along the satellite track directly in the altimetry L2 data.
The altimetry data selected for the study (Jason-2, Jason-3, and Sentinel-3A) include observations between February 1st and 5th, 2017. The area of the analysis is located in the EIA region, which is challenging in the modeling, especially from the sparse data. However, the period selected does not include enhanced solar activity (solar radio flux at F10.7 was dropping slowly from 77 s.f.u.), and TEC magnitudes are moderate. The length of the coastline, together with equatorial TEC properties, makes this region interesting for coastal studies of ionospheric corrections. Additional occurrence of large Mean Dynamic Topography (MDT) variability can make the observations from this area interesting for studies related to atmospheric corrections.
3. Review of GIMs in the coastal region where Equatorial Ionization Anomaly (EIA) occurs, with respect to ionospheric correction
The assessment of the ionospheric corrections from the altimeters and GIMs starts from the comparative assessment of this quantity along the selected trajectories of 3 altimetric satellites. The TEC values at the time and place of the selected tracks (low latitudes in 2017) are typically between 20-40 TECU, which is 4 times smaller than typical values, e.g., in the year 2002 (TEC in 2002 locally reached 150 TECU and solar radio flux at F10.7 varied from 140 to 260 s.f.u.). This means that the ionospheric correction values, as well as differences between their estimates from different sources, can be larger than the ones determined in this study. Therefore, this study refers to average conditions in terms of TEC and ionospheric delay size.
First, five profiles of satellite tracks having the largest differences between altimetry-derived ionospheric corrections and those interpolated and calculated from the GIMs are analyzed. Figures 3-5 show along-track ionospheric corrections from the altimetry and the five selected TEC models. The ionospheric corrections from dual-frequency altimeters placed onboard three satellites are filtered by the median filter with an 80 s window, and then compared with the corrections calculated from the GIMs. As noted, JPLG GIM is available as a standard GIM model for Ku-band and C-band ionospheric corrections in the Level 2 altimetry data, and therefore we took its values directly from the altimetry data files. The surface flags available in L2 altimetry data are used to indicate the occurrence of the land, but they indicate only coastal land in the case of S3A, as the data come from a marine data set, where land is excluded (Fig. 5b-f, right). The flags indicate the locations of the land in Figures 3-5. The left sub-figures in Figures 3-5 (b-f) present TEC interpolated along the track from the PPPLSC model to review its proportional relation with ionospheric correction. The right sub-figures in Figures 3-5 (b-f) show the size of the ionospheric delay that affects range measurements. It should be pointed out that TEC here values reach only 40 TECU, but can reach or exceed 100 TECU in more active solar phases.
Fig. 3.
a) Selected tracks of Jason-2 having the largest analyzed differences between Ku-band ionospheric corrections from altimetry and GIMs. b-f) Along-track TEC values interpolated from the PPPLSC model (left). Ionospheric corrections for Ku-band along selected passes (right) from filtered dual-frequency altimetry (black), JPLG GIM available in altimetric L2 datasets (brown) and interpolated from PPPLSC (red), UQRG (magenta), IGSG (blue) and CODG (green). Light brown bars show land derived from surface flags.
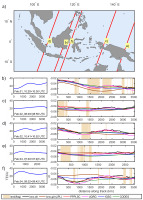
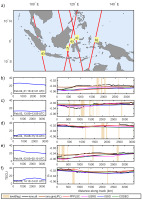
Fig. 5.
The same as in Fig. 3 but for the Sentinel-3A satellite. Light brown bars show land derived from surface flags, but only in coastal regions for S3A, because marine data with excluded land is used.
Figures 3b-f present ionospheric delays reaching 7-8 cm in the case of the largest TEC values (30-40 TECU). The black curves representing altimetry-derived delays are the most detailed, as they were not modeled, but only filtered. Thus, altimetry-derived ionospheric delays include the largest amount of the signal at the high-frequencies, unavailable in the case of GIMs. This finding also means that the filtering of altimetry-derived ionospheric delays by the moving average with an 80 s window still preserves more high frequencies than GIM models. This is true if we are aware that this window spans 400-500 km, whereas the GIMs are based on very sparse data in the oceans. Therefore, even stochastic modeling, although it can be more accurate in the least-squares sense, cannot extend the resolution. Additionally, the true resolution represented by spherical harmonics of degree 15 is much worse than 1000 km. Knowing the nature of stochastic modeling methods, like different types of kriging, we can expect more local details from PPPLSC and UQRG models than from JPLG, CODG, and IGSG, but rather in continental or coastal areas. This is confirmed especially in Figures 3d and 3f, where TEC from different models differs more along the Jason-2 tracks. The altimetry-derived delays have more composed curvatures along these trajectories, and PPPLSC and UQRG follow these curves, but the remaining three models (JPLG, CODG, and IGSG) do not follow these shapes and are flatter. Surprisingly, JPLG ionospheric delay is the most divergent from the altimetric one, which suggests that it is not the best choice as a supplement for altimetry; the values diverge in the coastal regions by as much as 3 cm. Such differences are larger than the total ionospheric correction at some higher latitudes or at some other time of the day. In the case of lower TEC values (around 20 TECU), the differences between different sources of ionospheric delay reach nearly 2 cm (Fig. 3c and 3e), which is almost half of the ionospheric delay itself.
The case of Jason-3 (Fig. 4) confirms the smoothness and lower order of spatial details of JPLG, CODG, and IGSG with respect to altimetry-derived delays, as well as more fitted shapes of the stochastic-based models (Fig. 4d and 4f). This fit is assessed based on the altimetry-derived delay, which includes the highest frequencies of the signal. The worst correspondence of JPLG with altimetry-derived delays is also again noticeable (Fig. 4e and 4f). The altimetry-based ionospheric delay from Jason-3 is even more divergent from the values interpolated from all the selected models, which can indicate some bias; this bias will also be confirmed in Section 4. The differences between the altimetry and GIMs in ionospheric delay units reach 2-3 cm, and it should be recalled that we are not working with the highest TEC values.
The selected Sentinel-3A trajectories represent slightly lower levels of TEC, and this turned out to be helpful in the assessment of GIMs under conditions of calmer TEC behavior. Contrary to Figures 3-4, Figures 5b and 5e indicate better correspondence of the JPLG model with dual-frequency altimeter measurements along the selected tracks. Figures 5c-d and 5f show TEC values below 20 TECU, when the delay is small. These examples are very useful in the analysis because they prove that harmonic modeling can be effective only under conditions of lower TEC variability. From previous observations (Figures 3-4), where we have a more pronounced EIA crest and better performance of stochastic models, it can be concluded that GIMs based on the spherical basis functions need more harmonic degrees in the EIA regions.
4. Ionospheric correction from altimetry vs. that from GIMs – results in EIA coastal regions
All the available along-track satellite footprints for 5 days in the selected coastal area are summarized in this section to measure the scale of discrepancies between different types of ionosphere models and different altimeters. The statistical values are calculated under conditions of moderate TEC with respect to the phase of the solar cycle, but the most variable with respect to the latitude, as located in the EIA region. The differences between ionospheric delay from 3 altimetry satellites and that interpolated along the tracks from 5 TEC models are calculated. Then minima, maxima, standard deviation, and RMS of differences are calculated for all models and satellites (Table 1). However, the graphics are limited only to TEC models having extreme differences (UQRG and JPLG) and the local author’s model PPPLSC (Fig. 6-8) to avoid figures showing comparable values. Overall, the ionospheric delay differences between altimetry and GIMs, and also between the GIMs themselves, reach 2-3 cm in the case of TEC at ~30 TECU. The study is performed in the region of EIA, and therefore the size of ionospheric corrections, as well as differences between different models, would be smaller at higher latitudes. On the other hand, TEC values can reach 100 TECU in times of stronger solar activity or ionospheric storms, and the discrepancies can be much larger than 3 cm. For this reason, the improvement of GIM accuracy for ionospheric delay calculation in altimetry is still an open challenge. We have to remember that there is an increased need for the application of GIMs in the coastal region, as the ionospheric correction can be affected by land in the altimeter footprint (Andersen, Scharroo 2011).
Fig. 6.
Differences of ionospheric corrections between Jason-2 altimetry-derived (Ku-band) and the corrections interpolated from 3 selected GIMs (JPL, PPPLSC, and UQRG).
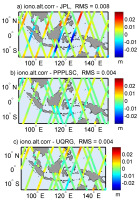
Table 1.
All statistical values from the comparison of ionospheric corrections from 3 altimeters and 5 GIMs (meters). Jason-2 Min.
Figures 6-8 present the comparisons of ionospheric delay along the tracks of 3 satellites and for 3 out of 5 models, and their basic statistical value, RMS. Two of these GIMs indicate extreme statistics (best and worst RMS), whereas the third plotted model is the author’s PPPLSC. Five days of observations, taken for the comparisons and calculated RMS, confirm previous findings related to GIM included in altimetric Level 2 products (JPLG). Figures 6-7 show worse fits of Jason-2 and Jason-3 with the JPL model and better consistency with PPPLSC and UQRG. A different result can be found in Figure 8, where JPLG performs similarly to the other two models. However, we note that Sentinel-3A passes over the selected region on the selected days were at a time of lower and much less variable TEC. The suggestion is that low-order harmonics of JPLG are determined with good accuracy, and the deficiency in higher-order terms limits the real total resolution of the JPLG model in terms of high-order details.
Table 1 presents 6 statistical values referring to the 5-day comparison of ionospheric delays from the altimetry and GIMs. At the beginning, we note that means and medians do not exceed 3 mm for Jason-2 and 5 mm for Sentinel-3A, and this refers to all TEC models. Thus, the systematic bias between GIMs and these two satellites does not exceed 2.5 TECU in the selected region. However, the means and medians in comparison of GIMs with Jason-3 approach 9 mm, which is close to 4.5 TECU. Nevertheless, the mean and median of differences between Jason-3 and PPPLSC is 5.5 mm, which means that it is possible to be closer with mean value to Jason-3, namely <3 TECU. Overall, the lowest standard deviations and RMS are found in the comparison between UQRG and PPPLSC, but this is valid for Jason-2 and Jason-3, where a more significant influence of EIA has been found along the altimetric tracks. The indication is that this region needs more than 15 spherical harmonic degrees in the interpolation of TEC in the EIA region or the application of stochastic techniques. The comparison with Sentinel-3A is likely to confirm this, as the RMS and standard deviations are very comparable for all TEC models in the case of comparison with this satellite, contrary to Jason satellites, where EIA is more evident. Referring to maxima and minima in comparison with Sentinel-3A, we see that although they decreased with respect to the comparison with Jason-2 and Jason-3, their values still reach or even exceed 2 cm. On the other hand, the normal distribution of the residuals, which is most frequently observed in the statistics, can suggest multiplying the standard deviation at least by 2, to obtain a representative size of the errors at a 95% confidence level. This would give approximately 2 cm errors between the altimetry and GIMs, when the ionospheric delay for the Ku-band would be 6 cm, equivalent to 30 TECU. This is one-third of the ionosphere correction for the altimetry.
5. Conclusions
The ionospheric correction filtered from dual-frequency altimetry retains more high-resolution information about the ionosphere along the satellite track than can be interpolated from the GIM. The reasons are (1) the sparse distribution of ground GNSS over the ocean, and (2) modeling with spherical basis functions, e.g., spherical harmonics. This study indicates that low-order spherical basis functions generate unacceptably large errors, which, when used for inland altimetry, can adversely affect the equatorial regions more than stochastic modeling of these delays. Therefore, the profiles of ionospheric delays interpolated from the models based on stochastic techniques (PPPLSC, UQRG) have shapes most comparable to altimetry-derived delays in the close vicinity of EIA. The stochastic modeling techniques can provide advantages in real resolution and accuracy, especially in regions of denser data, like continental and coastal regions. Together with the difference in real spatial resolution between the altimetric observation of Ku-band ionospheric delay, and interpolation of this delay from the GIM, we observe significant discrepancies between these two sources, up to 30% of the entire ionospheric correction. Namely, the differences between ionosphere corrections from different sources reach 2-3 cm in the case of TEC, ~30-35 TECU. The magnitude of TEC was moderate there at that time of the solar cycle, but the data were selected from the EIA region. Therefore, ionosphere corrections and differences between the models can be larger in the case of stronger solar activity with greater TEC. We can also expect correspondingly larger discrepancies in ionospheric delay acquired from different data sources.
Knowing that ionospheric delay from the GIMs can be subject to errors of several cm, the selection of GIM complementary to dual-frequency altimetry requires special care in coastal areas. Coastal and inland altimetry, along with the ionosphere corrections, can be extremely hard to assess from dual-frequency altimeters, especially over inland waters. Inland altimetry should undergo extensive progress in the coming years, when the planned SWOT mission, with the next generation of altimeter, will be a substantial milestone in the field. The GIMs are better over land because inland regions usually have dense GNSS station coverage. Nevertheless, the bias between the GIM and altimetry has to be eliminated, along with that from the modeling errors. The removal of the plasmaspheric TEC from the GIMs is also crucial, as there are some additional electrons to remove, especially above the 800 km orbit of Sentinel satellites.
The generally recommended actions for gaining more consistency between dual-frequency altimetry and GIMs, and assuring, say, compatibility at the level of 6 mm for the Ku-band (3 TECU), are constant employment of new GNSS ground stations and all other available data in GIM creation. The selection of the data must include a range of satellite data: DORIS, topside TEC from POD, occultation data, and also altimetry because ground data will never be sufficiently dense in the open ocean. It is also important to keep some data unused for validation purposes. The best validation data would be of high accuracy, and redundant at the specified location, so that their removal does not affect the models. Being aware of the unavoidable data gaps, the modeling techniques must be carefully selected, and implementation of stochastic techniques is advised, at least in combination with spherical basis functions. Another recommendation worth consideration follows from the validation of GIM models by the satellite altimetry tracks. Namely, the fitting of a GIM model into altimetry-derived TEC could be considered, to obtain a coincident reference level suitable for altimetry and other applications. A similar solution was extensively used in geodesy for the gravimetric geoid models, which were fitted to independent geometric geoid values coming from leveling and GNSS positioning. By these means, the continuous surface from the GIM can achieve the reference level compatible with TEC measured by the altimeter.